
FAQ algorithmesConsultez toutes les FAQ
Nombre d'auteurs : 6, nombre de questions : 125, dernière mise à jour : 23 août 2017 Ajouter une question
Cette FAQ a été réalisée à partir des questions fréquemment posées sur les forums de Developpez.com et de l'expérience personnelle des auteurs.
Nous tenons à souligner que cette FAQ ne garantit en aucun cas que les informations qu'elle propose sont correctes ; les auteurs font le maximum, mais l'erreur est humaine. Cette FAQ ne prétend pas non plus être complète. Si vous souhaitez devenir rédacteur, lisez ceci. Vous pouvez poster toutes vos remarques, questions, avis et corrections sur la FAQ sur le forum.
Nous espérons que cette FAQ saura répondre à un maximum de vos questions. Nous vous souhaitons une bonne lecture.
L'équipe algorithmique de Developpez.
 2.1. Algorithmes de tri
(4)
2.1. Algorithmes de tri
(4)
- Qu'est-ce qu'un algorithme ?
- Qu'est-ce que l'ordre lexicographique ?
- Qu'est-ce qu'une permutation de n éléments ?
- Qu'est-ce qu'un arrangement de p éléments parmi n ?
- Qu'est-ce qu'une combinaison de p éléments parmi n ?
- Qu'est-ce que l'ensemble des parties d'un ensemble ?
- Quand dit-on qu'un algorithme est totalement correct ?
- Qu'est-ce qu'une structure de données ?
- Quand dit-on qu'un algorithme est récursif ?
- Qu'est-ce qu'une assertion ?
- En quoi consiste la preuve par induction ?
Un algorithme consiste en la spécification d'un schéma de calcul, sous forme d'une suite d'opérations élémentaires obéissant à un enchaînement déterminé.
L'ordre lexicographique est un ordre total sur les listes d'éléments de même type :
- si deux listes sont vides alors elles sont égales ;
- si une liste est vide alors elle est plus petite que l'autre ;
- sinon on compare les deux têtes de liste ;
- si elles sont différentes alors on renvoie le résultat de la comparaison ;
- sinon on compare les deux queues.
L'ordre lexicographique appliqué aux chaînes de caractères est simplement l'ordre alphabétique.
Soit S un ensemble possédant n éléments. Une permutation de l'ensemble S est une séquence (un ensemble ordonné) des n éléments de S.
Par exemple, le quintuplet (1,4,3,2,5) est une permutation de l'ensemble {1,2,3,4,5}.
Le nombre de permutations d'un ensemble à n éléments est donné par la formule : P(n) = n!
Soit S un ensemble possédant n éléments. Un arrangement de p éléments de l'ensemble S est une séquence (un ensemble ordonné) de p éléments de S.
Par exemple, le triplet (2,4,5) est un arrangement de 3 éléments de l'ensemble {1,2,3,4,5}. Le triplet (5,2,4) est un autre arrangement possible de 3 éléments du même l'ensemble.
Le nombre d'arrangements de p éléments d'un ensemble à n éléments est donné par la formule : A = (n)! / (n-p)!
Remarque : un arrangement de n éléments parmi n est une permutation de n éléments.
Soit S un ensemble possédant n éléments. Une combinaison de p éléments de S est une partie de S possédant p éléments.
Par exemple, l'ensemble {2,4,5} est une combinaison de 3 éléments de l'ensemble {1,2,3,4,5}.
Le nombre de combinaisons de p éléments d'un ensemble à n éléments est donné par la formule : C = (n)! / ((n-p)!(p)!).
Soit S un ensemble possédant n éléments. L'ensemble des parties de S se note P(S) et contient tous les ensembles inclus dans S, y compris l'ensemble vide et l'ensemble S lui-même.
Exemple : si S = {1,2,3} alors P(S) = {{},{1},{2},{3},{1,2},{2,3},{1,3},{1,2,3}}.
Remarques :
- P(S) est l'ensemble de toutes les combinaisons de p éléments de S pour p variant de 0 à n ;
- P(S) possède 2^(n) éléments.
Un algorithme est dit totalement correct lorsque, pour chaque instance d'un problème, il se termine en produisant la bonne sortie.
Un algorithme est dit partiellement correct si, quand il se termine, il donne la bonne sortie, sans assurer qu'il se termine.
Une structure de données est une méthode de stockage et d'organisation des données pour en faciliter l'accès et la modification. Elle regroupe des données à gérer et un ensemble d'opérations que l'on peut leur appliquer. En général, il existe plusieurs manières de représenter ces données et plusieurs implémentations de leur manipulation.
Parmi les structures de données les plus courantes, on compte les tableaux, les listes chaînées, les piles et les files. Les arbres et les graphes sont aussi beaucoup utilisés.
Un algorithme est dit récursif s'il s'invoque lui-même (directement ou non – récursif multiple). Cela permet de simplifier l'expression de certains algorithmes.
Une procédure sera récursive terminale si elle n'effectue plus aucune opération après s'être invoquée récursivement.
Une assertion est une relation entre les variables qui est vraie à un moment dans l'exécution. Notamment, on compte les pré et postconditions (conditions que doivent remplir les données d'entrée et de sortie) 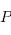 et
et 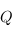 .
.
La preuve par induction se passe en deux étapes :
- cas de base : on montre explicitement que la propriété est vraie pour une série d'instances ;
- cas inductif : on suppose que la propriété est vraie pour les instances précédentes du problème et on montre qu'elle l'est aussi pour l'instance suivante.
Cette manière de procéder est correcte pour tout ensemble bien ordonné. Par exemple, l'ensemble des naturels
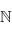 est bien ordonné par la relation
est bien ordonné par la relation 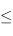 : dans tout sous-ensemble non vide de
: dans tout sous-ensemble non vide de 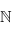 , il y a un plus petit élément.
, il y a un plus petit élément. Proposer une nouvelle réponse sur la FAQ
Ce n'est pas l'endroit pour poser des questions, allez plutôt sur le forum de la rubrique pour çaLes sources présentées sur cette page sont libres de droits et vous pouvez les utiliser à votre convenance. Par contre, la page de présentation constitue une œuvre intellectuelle protégée par les droits d'auteur. Copyright © 2026 Developpez Developpez LLC. Tous droits réservés Developpez LLC. Aucune reproduction, même partielle, ne peut être faite de ce site et de l'ensemble de son contenu : textes, documents et images sans l'autorisation expresse de Developpez LLC. Sinon vous encourez selon la loi jusqu'à trois ans de prison et jusqu'à 300 000 € de dommages et intérêts.




