
FAQ algorithmesConsultez toutes les FAQ
Nombre d'auteurs : 6, nombre de questions : 125, dernière mise à jour : 23 août 2017 Ajouter une question
Cette FAQ a été réalisée à partir des questions fréquemment posées sur les forums de Developpez.com et de l'expérience personnelle des auteurs.
Nous tenons à souligner que cette FAQ ne garantit en aucun cas que les informations qu'elle propose sont correctes ; les auteurs font le maximum, mais l'erreur est humaine. Cette FAQ ne prétend pas non plus être complète. Si vous souhaitez devenir rédacteur, lisez ceci. Vous pouvez poster toutes vos remarques, questions, avis et corrections sur la FAQ sur le forum.
Nous espérons que cette FAQ saura répondre à un maximum de vos questions. Nous vous souhaitons une bonne lecture.
L'équipe algorithmique de Developpez.
- Qu'est-ce qu'un arbre binaire ?
- Qu'est-ce qu'un arbre binaire dégénéré ?
- Qu'est-ce qu'un arbre binaire équilibré ?
- Qu'est-ce qu'un arbre binaire complet ?
- Qu'est-ce que le nombre de Strahler d'un arbre binaire ?
- Qu'est-ce que la racine d'un arbre ?
- Qu'est-ce que le niveau de rang n d'un arbre binaire ?
- Qu'est-ce que la profondeur d'un nœud ?
- Qu'est-ce que la hauteur d'un arbre binaire ?
- Qu'est-ce que le parcours préfixe/infixe/postfixe d'un arbre binaire ?
- Qu'est-ce qu'un parcours d'un arbre binaire à gauche (à droite) d'abord ?
- Qu'est-ce qu'un arbre binaire de recherche ?
- Qu'est-ce qu'un arbre AVL ?
- Qu'est-ce qu'un arbre rouge-noir ?
- Qu'est-ce qu'un splay-arbre ?
- Qu'est-ce qu'un arbre n-aire ?
- Comment implanter un arbre n-aire ?
- Qu'est-ce qu'un trie ou arbre Patricia ?
- Qu'est-ce qu'un arbre ternaire ?
- Qu'est-ce qu'un quadtree ?
- Qu'est-ce qu'un octree ?
- Qu'est-ce qu'un KD-tree ?
- Qu'est-ce que la propriété de tas ?
- Qu'est-ce qu'un tas binaire ?
- Qu'est-ce qu'un splay-tas ?
- Qu'est-ce qu'un arbre binomial ?
- Qu'est-ce qu'un tas binomial ?
- Qu'est-ce qu'un arbre de Fibonacci ?
- Qu'est-ce qu'une liste à accès aléatoire ?
- Qu'est-ce qu'un arbre de Braun ?
- Qu'est-ce qu'un arbre ?
- Qu'appelle-t-on arité d'un arbre ?
- Qu'est-ce qu'un nœud ?
- Qu'appelle-t-on degré d'un nœud ?
- Qu'appelle-t-on taille d'un arbre ?
- Qu'appelle-t-on profondeur d'un nœud ?
- Qu'appelle-t-on hauteur d'un arbre ?
- Quand dit-on qu'un arbre est binaire ?
- Quand dit-on qu'un arbre est parfait ou complet ?
- Qu'appelle-t-on arbre binaire entier ou propre (full ou proper) ?
- Qu'est-ce qu'un arbre binaire localement complet ?
- Qu'est-ce qu'un arbre dégénéré ?
- Qu'est-ce qu'un arbre binaire complet ?
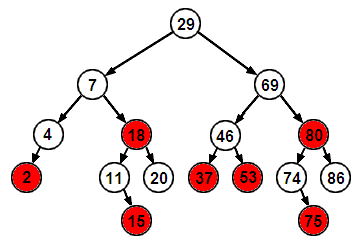
Un arbre binaire étiqueté est :
- ou bien une feuille (un arbre vide) ;
- ou bien un nœud (une cellule d'arbre portant une étiquette et ayant pour fils deux arbres binaires étiquetés).
Dans la plupart des implantations un singleton (null ou un équivalent) joue le rôle de feuille. Par convention l'un des deux fils d'un nœud sera appelé sous-arbre à gauche (ou fils gauche) et l'autre sous-arbre à droite (ou fils droit).
Un exemple d'arbre binaire (où l'on n'a pas fait figurer les étiquettes) :
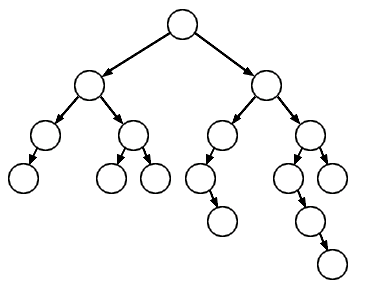
Un arbre binaire dégénéré est un arbre binaire tel que le nombre de noeuds dans le fils gauche peut être arbitrairement plus petit ou plus grand que le nombre de nœuds dans le fils droit.
Un arbre binaire équilibré est un arbre binaire qui ne peut jamais être ou devenir dégénéré.
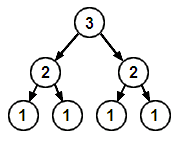
- Une feuille est un arbre binaire complet de rang 0.
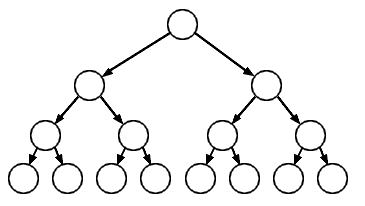
- Un arbre complet de rang n > 0 est un nœud ayant pour fils deux arbres binaires complets de rang n-1.
Du fait de l'identité de rang entre ses deux sous-arbres un arbre binaire complet est un arbre équilibré. Un arbre complet de rang n contient 2^(n)-1 nœuds.
Un arbre binaire complet de rang 4 :
- Le nombre de Strahler d'une feuille est égal à 1.
- Soient sl et sr les nombres deStrahler de deux sous-arbres d'un nœud :
- si sl = sr alors le nombre de Strahler du nœud est sl + 1 ;
- sinon le nombre de Strahler du nœud est max(sl,sr).
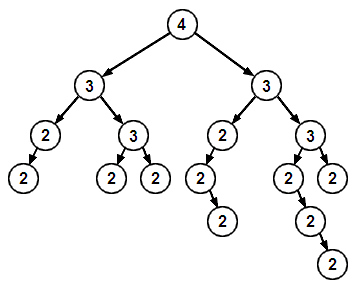
Le nombre de Strahler est une métrique pour l'équilibre d'un arbre binaire. On a en particulier les deux cas limites suivants :
- le nombre de Strahler d'un arbre binaire complet de rang n est égal à n+1 ;
- le nombre de Strahler d'un arbre binaire dégénéré de profondeur n tend vers 1.
Plus généralement, le nombre de Strahler est une métrique de la complexité de branchement dans un arbre n-aire.
Un arbre binaire où chaque nœud a été étiqueté avec son nombre de Strahler :
La racine d'un arbre non vide est l'unique nœud qui n'est le fils d'aucun autre nœud.
On dit qu'un nœud est sur le niveau de rang n d'un arbre binaire si le chemin qui mène de ce nœud à la racine compte exactement n+1 nœuds.
On dit qu'un nœud est de profondeur n dans un arbre binaire si le chemin qui mène de ce nœud à la racine compte exactement n nœuds.
Un arbre binaire complet de rang 3 où chaque nœud a été étiqueté avec sa profondeur :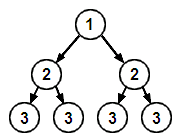
- Si l'arbre est une feuille alors sa hauteur est 0.
- Sinon sa hauteur est la profondeur maximale de l'ensemble de ses nœuds.
Une autre définition, par induction :
- une feuille est un arbre binaire de hauteur 0 ;
- un arbre binaire de hauteur n>0 est un arbre binaire dont la hauteur du sous-arbre le plus haut (celui à gauche ou celui à droite) est égale à n-1.
Un arbre binaire complet de rang 3 où chaque nœud a été étiqueté avec la hauteur de l'arbre correspondant :
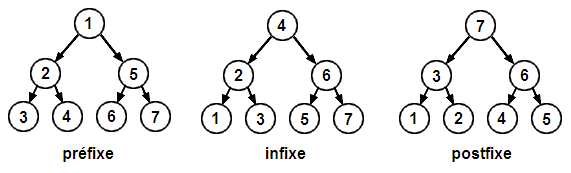
Le parcours (ou traversée) d'un arbre binaire étiqueté est l'action d'appliquer une fonction f à l'étiquette de chacun de ses nœuds.
Le parcours procède comme ceci :
- si l'arbre est une feuille alors on ne fait rien ;
- sinon on distingue trois stratégies pour le parcours d'un nœud ;
- en ordre préfixe : on applique f à l'étiquette, puis on explore le fils gauche, puis le fils droit ;
- en ordre infixe : on explore le fils gauche, puis on applique f à l'étiquette, puis on explore le fils droit ;
- en ordre postfixe : on explore le fils gauche, puis le fils droit, puis on applique f à l'étiquette.
Un arbre binaire où chaque nœud a été étiqueté avec son rang dans le parcours concerné :
Un parcours d'un arbre binaire à gauche d'abord est un parcours préfixe, infixe ou postfixe tel que précédemment défini.
Un parcours d'un arbre binaire à droite d'abord est un parcours préfixe, infixe ou postfixe tel que précédemment défini mais avec ceci pour différence que :
- là où l'on explorait à gauche on explorera à droite ;
- là où l'on explorait à droite on explorera à gauche.
Un arbre binaire ordonné (ou arbre binaire de recherche) est un arbre binaire étiqueté qui respecte l'invariant structurel suivant :
- pour tout nœud l'étiquette est un majorant pour le fils gauche et un minorant pour le fils droit.
Un exemple d'arbre binaire de recherche :
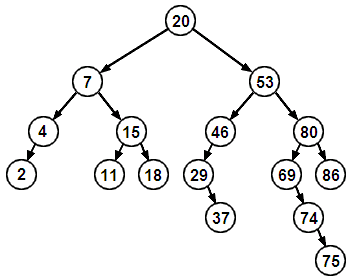
L'étiquette d'un nœud d'arbre binaire ordonné se comporte à la manière du pivot d'un quicksort, les étiquettes plus petites sont toujours à gauche, les étiquettes plus grandes sont toujours à droite.
Un arbre binaire de recherche équilibré de cardinalité n supporte les opérations suivantes (complexité dans le pire des cas) :
- l'insertion d'un élément en O(log n) ;
- la recherche d'un élément en O(log n) ;
- la suppression d'un élément en O(log n) ;
- la recherche du minimum et du maximum en O(log n) ;
- la recherche du i-ième élément en O(log n) (si en plus chaque nœud contient son cardinal) ;
- la partition selon un élément en O(log n) ;
- l'union avec un arbre de cardinalité m en O(n+m).
Un arbre binaire de recherche non équilibré peut devenir dégénéré. En conséquence on distingue deux cas pour un arbre binaire non équilibré :
- il devient dégénéré, dans ce cas les opérations de base deviennent de complexité O(n) dans le pire des cas, comme pour une liste chaînée ;
- il ne devient pas dégénéré, dans ce cas toutes les opérations de base deviennent de complexité amortie O(log n).
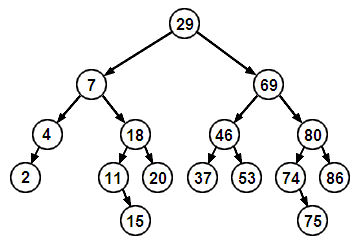
Un arbre AVL (Adelson-Velskii-Landis) est un arbre binaire de recherche qui maintient l'invariant structurel
suivant :
- la différence de hauteur entre son fils gauche et son fils droit est au plus égale à 1.
Du fait de cette contrainte un arbre AVL est forcément un arbre équilibré.
Cet invariant structurel est maintenu à l'aide de 4 transformations locales (2 rotations simples et 2 rotations doubles).
Un exemple d'arbre AVL :
Un arbre rouge-noir est un arbre binaire de recherche équilibré qui maintient l'invariant structurel suivant :
- tout nœud est soit rouge soit noir ;
- si un nœud est rouge alors il a un nœud père qui est noir ;
- tous les chemins menant de la racine à une feuille contiennent le même nombre de nœuds noirs.
En conséquence de ces contraintes un arbre rouge-noir est forcément un arbre équilibré.
Cet invariant structurel est maintenu à l'aide de 4 transformations locales (2 rotations simples et 2 rotations doubles).
Un exemple d'arbre rouge-noir :
Un splay-arbre est un arbre binaire de recherche adaptatif dont les opérations de recherche et d'insertion réalisent une réorganisation locale appelée splaying.
Cette opération de splaying a un double effet :
- elle tend à rendre l'arbre binaire plus équilibré ;
- elle place les éléments recherchés à la racine, ce qui introduit un effet de cache appréciable pour toutes les applications où la recherche n'est pas localement uniforme.
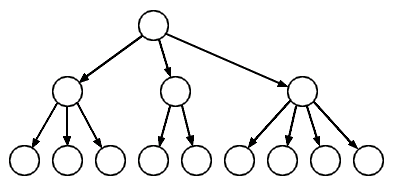
Un arbre n-aire étiqueté est :
- ou bien une feuille (un arbre vide) ;
- ou bien un nœud (une cellule d'arbre portant une étiquette et ayant pour fils 0 à n arbre(s) n-aire étiqueté(s)).
Un exemple d'arbre n-aire de profondeur 3 :
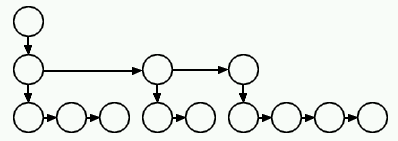
Une représentation simple et économique des arbres n-aire consiste à :
- représenter les nœuds à l'aide des nœuds d'un arbre binaire ;
- l'un des sous-arbres désigne les frères, l'autre désigne les fils.
Le même arbre n-aire de profondeur 3 implanté par un arbre binaire :
Remarque : dans cette représentation une forêt est simplement une fratrie d'arbres n-aires.
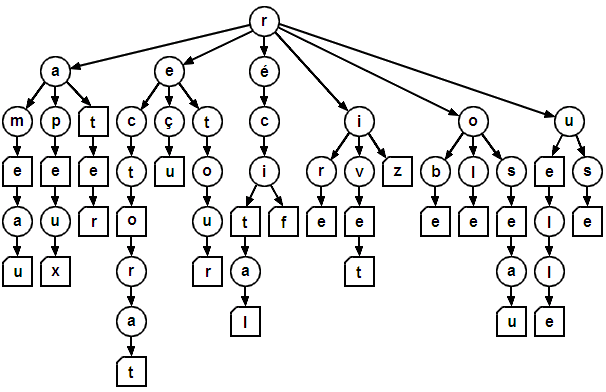
Un trie (ou arbre Patricia) est une structure de données ordonnée selon l'ordre lexicographique.
Un trie est un arbre multi-niveaux pour ordonner des listes :
- les étiquettes des nœuds sur le niveau de rang 0 discriminent l'élément de rang 0 dans la clé ;
- les étiquettes des nœuds sur le niveau de rang n discriminent l'élément de rang n dans la clé ;
- les nœuds terminaux testent la fin de la clé (et contiennent l'information associée si le trie est un conteneur associatif).
Un exemple de trie (les nœuds carrés signalent la dernière lettre d'un mot du lexique) :
Un arbre ternaire est un trie implanté comme un arbre binaire de recherche étiqueté auquel on a ajouté un champ supplémentaire. Ce champ supplémentaire est le trie de rang n+1 et correspond au cas où l'étiquette du nœud coïncide avec l'élément de rang n dans la clé. Un arbre ternaire est une sorte d'hybride entre un arbre binaire ordonné et une liste chaînée :
- la recherche de l'élément de rang n se fait comme la recherche dans un arbre binaire ordonné ;
- le passage de l'élément de rang n à l'élément de rang n+1 se fait comme la progression dans une liste.
Un quadtree est une structure de données pour la division partiale d'une partie du plan.
Un quadtree divise (récursivement) une portion finie du plan en quatre quadrants de tailles égales.
Un octree est une structure de données pour la division partiale d'une partie de l'espace en trois dimensions.
Un octree divise (récursivement) une portion finie de l'espace en huit octants de tailles égales.
Un KD-tree est une structure de données pour la division spatiale de l'espace en K dimensions. Un KD-tree est implanté comme un arbre binaire de recherche multi-niveaux.
Un KD-tree non dégénéré de cardinalité n supporte les opérations suivantes (en complexité amortie) :
- l'insertion d'un point en O(log n) ;
- la recherche d'un point en O(log n) ;
- la recherche du contenu d'un hyper-cube en O(log n) (le contenu du cube est supposé petit par rapport à n) ;
- la recherche du plus proche voisin S d'un point C en O(log n) (on suppose que C n'est pas le centre d'une hyper-sphère vide de rayon CS dont la majorité des n points sont proches de sa surface).
Remarque : le KD-tree est très utilisé en géométrie algorithmique pour la recherche dans un ensemble de points.
La propriété de tas-min pour un arbre étiqueté est l'invariant structurel suivant :
- toute étiquette d'un nœud est un minorant pour ses sous-arbres.
La propriété de tas-max pour un arbre étiqueté est l'invariant structurel suivant :
- toute étiquette d'un nœud est un majorant pour ses sous-arbres.
Un tas binaire est un arbre binaire qui vérifie la propriété de tas.
Un exemple de tas binaire minimum :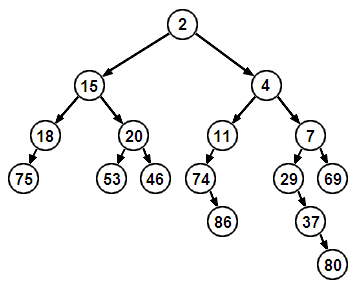
Un splay-tas est une structure de tas adaptative dont les opérations de recherche et d'insertion réalisent une réorganisation locale appelée splaying.
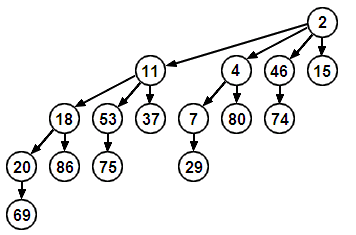
- Une feuille est un arbre binomial de rang 0.
- Un arbre binomial de rang n > 0 est un noeud ayant n fils de rangs décroissants n-1,n-2,...,0. Ou, de façon équivalente, un arbre binomial de rang n > 0 est un arbre binomial de rang n-1 auquel on a ajouté un autre arbre de rang n-1 comme fils le plus à gauche.
Un arbre binomial de rang n contient 2^(n) nœuds.
Un exemple d'arbre binomial de rang 4 qui vérifie la propriété de tas-minimum :
Le même arbre binomial de rang 4 implémenté à l'aide d'un arbre binaire :
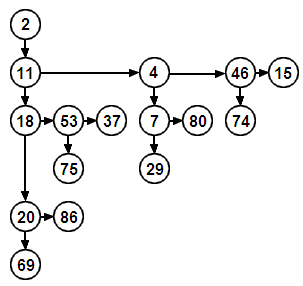
Un tas binomial est une structure de tas implantée à l'aide d'une forêt binomiale et dont chacun des arbres binomiaux vérifie la propriété de tas. Un tas binomial offre les performances suivantes (cas du tas-min, complexité dans le pire des cas) :
- insertion d'un l'élément en O(log n) (ou en O(1) à l'aide d'un curseur sur le minimum) ;
- recherche de l'élément minimum en O(log n) ;
- suppression de l'élément minimum en O(log n) ;
- union avec un autre tas-min en O(log n).
Un tas binomial non persistant peut offrir en plus les opérations suivantes :
- suppression d'un élément quelconque dans le tas en O(log n) ;
- réaffectation d'un élément à une position inférieure en O(log n).
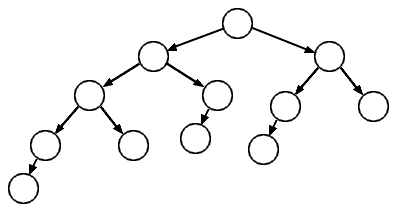
- un arbre de hauteur 0 est un arbre de Fibonacci de rang 0 ;
- un arbre de hauteur 1 est un arbre de Fibonacci de rang 1 ;
- un arbre de Fibonacci de rang n > 1 est un nœud dont le fils gauche est un arbre de Fibonacci de rang n-1 et le fils droit est un arbre de Fibonacci de rang n-2
Un arbre de Fibonacci de rang 5 :
Une liste à accès aléatoire est une structure de liste implantée à l'aide d'une forêt d'arbres binaires complets ordonnés selon le rang des éléments dans la liste.
Une liste à accès aléatoire de cardinal n offre toutes les opérations habituelles pour les listes chaînées, plus l'accès à l'élément de rang i en un temps O(min (i,log n)) dans le pire des cas.
Un arbre de Braun est un arbre binaire qui respecte l'invariant structurel suivant :
- si son fils gauche contient n nœuds alors son fils droit en contient ou bien n ou bien n-1.
Du fait de cette contrainte un arbre de Braun est forcément un arbre équilibré. Les arbres de Braun servent à implanter les tableaux de taille flexible.
Autres propriétés des arbres de Braun :
- un arbre de Braun de hauteur n+1 est complet sur ses n premiers niveaux ;
- l'indice d'un nœud dans un arbre de Braun est un minorant des indices de ses nœuds enfants.
Un exemple d'arbre de Braun (les nœuds sont étiquetés avec leur indice dans le tableau flexible) :
Un arbre est un graphe dirigé constitué d'un ensemble de nœuds reliés par des arcs. Ce graphe est connexe et acyclique. S'il est non vide, alors il possède un nœud distingué et unique, la racine.
On distingue deux grands types d'arbres : les arbres enracinés et les arbres non enracinés.
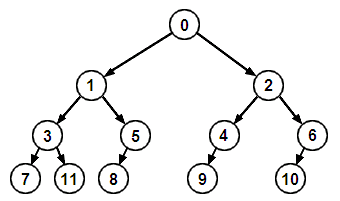
Un arbre enraciné est un arbre hiérarchique dans lequel on peut établir des niveaux. Il ressemblera plus à un arbre généalogique tel qu'on le conçoit couramment. Voici un exemple d'arbre enraciné :
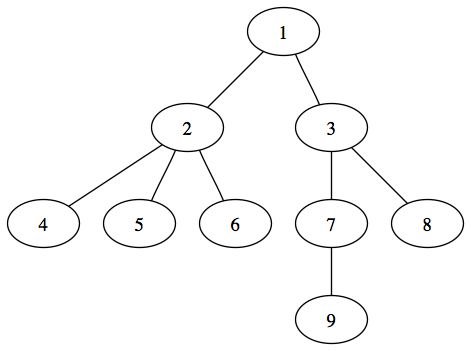
Dans un arbre non enraciné, il n'y a pas de relation d'ordre ou de hiérarchie entre les éléments qui composent l'arbre. On peut passer d'un arbre non enraciné à un arbre enraciné. Il suffit de choisir un élément comme sommet de l'arbre et de l'organiser de façon à obtenir un arbre enraciné. Voici un exemple d'arbre non enraciné :
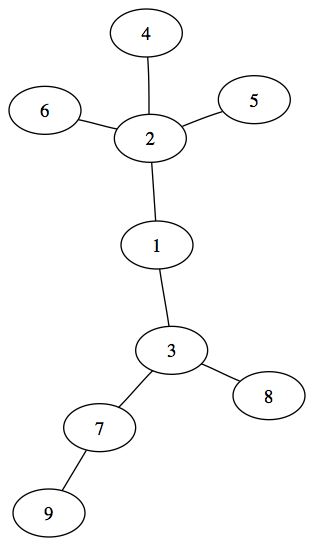
On a aussi envie de qualifier un arbre sur le nombre de fils qu'il possède. Ceci s'appelle l'arité de l'arbre. Un arbre dont les nœuds ne comporteront qu'au maximum n fils sera d'arité n. On parlera alors d'arbre n-aire. Il existe un cas particulièrement utilisé : c'est l'arbre binaire. Dans un tel arbre, les nœuds ont au maximum deux fils. On parlera alors de fils gauche et de fils droit pour les nœuds constituant ce type d'arbre.
L'arité n'impose pas le nombre minimum de fils, il s'agit d'un maximum, ainsi un arbre d'arité 3 pourra avoir des nœuds qui ont 0,1,2 ou 3 fils, mais en tout cas pas plus.
Précisons maintenant un peu plus les termes désignant les différents composants d'un arbre.
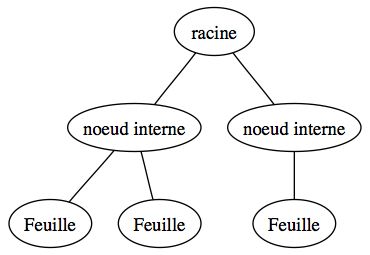
Tout d'abord, chaque élément d'un arbre se nomme un nœud. Les nœuds sont reliés les uns aux autres par des relations d'ordre ou de hiérarchie. Ainsi on dira qu'un nœud possède un père, c'est-à-dire un nœud qui lui est supérieur dans cette hiérarchie. Il possède éventuellement un ou plusieurs fils.
Il existe un nœud qui n'a pas de père, c'est donc la racine de l'arbre. Un nœud qui n'a pas de fils est appelé une feuille. Parfois on appelle une feuille un nœud externe, tout autre nœud de l'arbre sera alors appelé un nœud interne.
Voici donc un schéma qui résume les différents composants d'un arbre :
On appelle degré d'un nœud, le nombre de fils que possède ce nœud.
On appelle la taille d'un arbre, le nombre de nœuds internes qui le compose. C'est-à-dire le nombre total de nœuds moins le nombre de feuilles de l'arbre.
On appelle également la profondeur d'un nœud la distance en termes de nœud par rapport à l'origine. Par convention, la racine est de profondeur 0. Dans l'exemple suivant le nœud F est de profondeur 2 et le nœud H est de profondeur 3.
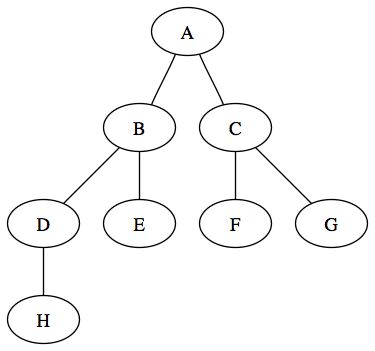
La hauteur d'un arbre est la profondeur maximale de ses nœuds. C'est-à-dire la profondeur à laquelle il faut descendre dans l'arbre pour trouver le nœud le plus loin de la racine. On peut aussi définir la hauteur de manière récursive : la hauteur d'un arbre est le maximum des hauteurs des fils.
En d'autres termes, la hauteur d'un arbre est la distance entre la feuille la plus éloignée et la racine.
Un arbre est dit binaire si chacun de ses nœuds possède au plus deux fils (un gauche et un droit, le gauche précédent le droit).
Un arbre est dit parfait ou complet si toutes ses feuilles sont à la même distance de la racine.
Un arbre binaire entier ou propre (full ou proper) est un arbre binaire dans lequel tous les nœuds internes possèdent exactement deux fils. Pour ces arbres, on dispose de quelques propriétés :
- le nombre de nœuds externes est égal au nombre de nœuds internes plus une unité ;
- le nombre de nœuds internes est égal à \[\frac{n-1}{2}\], où \[n\] est le nombre de nœuds ;
- le nombre de nœuds à la profondeur (niveau) \[i\] est inférieur ou égal à \[2^{i}\] ;
- la hauteur de l'arbre est inférieure ou égale au nombre de ses nœuds internes.
On peut lier la hauteur \[h\] et le nombre de nœuds \[n\] pour un arbre binaire entier par
\[n\in\Omega(h)\]
\[n\in O(2^{h})\]
De manière équivalente,
\[h\in O(n)\]
\[h\in\Omega(\log n)\]
Un arbre binaire localement complet est un arbre binaire dont chacun des nœuds possède soit 0, soit 2 fils. Cela veut donc dire que les nœuds internes auront tous deux fils. Dans ce type d'arbre, on peut établir une relation entre la taille de l'arbre et le nombre de feuilles. En effet, un arbre binaire localement complet de taille n aura n+1 feuilles. L'arbre suivant est localement complet :
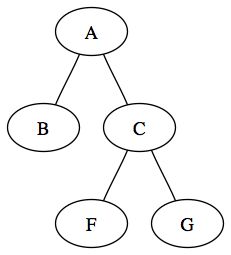
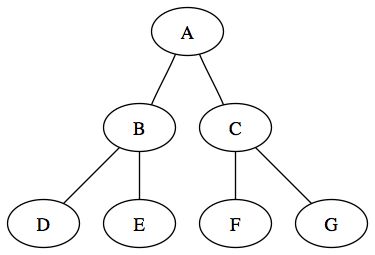
Un arbre dégénéré (appelé aussi filiforme) est un arbre dont les nœuds ne possèdent qu'un et un seul fils. Cet arbre est donc tout simplement une liste chaînée. Ce type d'arbre est donc à éviter, puisqu'il n'apportera aucun avantage par rapport à une liste chaînée simple. On a alors une relation entre la hauteur et la taille : un arbre dégénéré de taille n a une hauteur égale à n+1. L'arbre suivant est un arbre dégénéré :

On appellera arbre binaire complet tout arbre qui est localement complet et dont toutes les feuilles ont la même profondeur. Dans ce type d'arbre, on peut exprimer le nombre de nœuds n de l'arbre en fonction de la hauteur h : n = 2^(h+1) -1..
Proposer une nouvelle réponse sur la FAQ
Ce n'est pas l'endroit pour poser des questions, allez plutôt sur le forum de la rubrique pour çaLes sources présentées sur cette page sont libres de droits et vous pouvez les utiliser à votre convenance. Par contre, la page de présentation constitue une œuvre intellectuelle protégée par les droits d'auteur. Copyright © 2026 Developpez Developpez LLC. Tous droits réservés Developpez LLC. Aucune reproduction, même partielle, ne peut être faite de ce site et de l'ensemble de son contenu : textes, documents et images sans l'autorisation expresse de Developpez LLC. Sinon vous encourez selon la loi jusqu'à trois ans de prison et jusqu'à 300 000 € de dommages et intérêts.




