
FAQ algorithmesConsultez toutes les FAQ
Nombre d'auteurs : 6, nombre de questions : 125, dernière mise à jour : 23 août 2017 Ajouter une question
Cette FAQ a été réalisée à partir des questions fréquemment posées sur les forums de Developpez.com et de l'expérience personnelle des auteurs.
Nous tenons à souligner que cette FAQ ne garantit en aucun cas que les informations qu'elle propose sont correctes ; les auteurs font le maximum, mais l'erreur est humaine. Cette FAQ ne prétend pas non plus être complète. Si vous souhaitez devenir rédacteur, lisez ceci. Vous pouvez poster toutes vos remarques, questions, avis et corrections sur la FAQ sur le forum.
Nous espérons que cette FAQ saura répondre à un maximum de vos questions. Nous vous souhaitons une bonne lecture.
L'équipe algorithmique de Developpez.
- Qu'est-ce qu'un graphe orienté/non orienté ?
- Qu'est-ce qu'un arc/arête ?
- Qu'est-ce qu'un algorithme de plus court chemin ?
- Qu'est-ce qu'une boucle ?
- Qu'est-ce qu'un chemin/chaîne ?
- Qu'est-ce qu'un graphe connexe/fortement connexe ?
- Qu'est-ce qu'un cycle/circuit ?
- Qu'est-ce qu'un arbre ?
- Qu'est-ce qu'une forêt ?
- Qu'est-ce qu'un sous-graphe, qu'est-ce qu'un sous-graphe couvrant ?
- Qu'est-ce que le voisinage d'un nœud ?
- Que sont les ponts de Köenigsberg ?
- Qu'est-ce qu'un graphe complet ?
- Qu'est-ce qu'un graphe planaire ?
- Qu'est-ce qu'une clique ?
- Qu'est-ce qu'une k-clique ?
- Qu'est-ce qu'un stable ?
- Qu'est-ce qu'un graphe eulérien ?
- Qu'est-ce qu'un graphe hamiltonien ?
- Qu'est-ce qu'un parcours de graphe (en largeur, en profondeur) ?
- Qu'est-ce qu'un arbre couvrant ?
- Qu'est-ce que le problème du voyageur de commerce ?
- Qu'est-ce que le problème de coloration de graphe ?
- Qu'est-ce que le nombre chromatique ?
- Qu'est-ce que l'ordre d'un graphe ?
- Qu'est-ce qu'un graphe biparti ?
- Qu'est-ce que l'arité d'un nœud ?
- Qu'est-ce que le degré d'un nœud ?
- Qu'est-ce que le degré d'un graphe ?
- Qu'est-ce que l'incidence ?
- Qu'est-ce que le carré d'un graphe ?
- Qu'est-ce qu'un puit s?
- Qu'est-ce qu'une source ?
- Qu'est-ce qu'un sommet pendant ?
- Qu'est-ce qu'un ensemble dominant ?
- Qu'est-ce qu'un graphe acyclique ?
- Qu'est-ce qu'une partition ?
- Qu'est-ce que la valuation d'un graphe ?
- Qu'est-ce qu'un graphe régulier ?
- Qu'est-ce qu'un graphe cubique ?
- Qu'est-ce qu'un majorant/minorant ?
- Qu'est-ce que le maximum/minimum ?
- Qu'est-ce que la borne supérieure/inférieure ?
- Qu'est-ce qu'un élément maximal/minimal ?
- Qu'est-ce qu'une relation d'ordre ?
En théorie des graphes, on désigne par graphe deux types d'objets :
- les graphes orientés (digraph en anglais) ;
- les graphes non orientés (graph ou undirected graph en anglais) que l'on appelle parfois simplement graphe.
Formellement, un graphe orienté est un couple (S,A) où S est l'ensemble des sommets du graphe et A est l'ensemble des arcs du graphe. Chaque arc est un couple de sommets dont le premier élément est le sommet de départ de l'arc et le second élément est le sommet d'arrivée de l'arc.
Par exemple, une représentation graphique du graphe orienté G = (S,A) avec S = {A,B,C,D,F} et A = {(A,C), (A,B), (C,D), (D,A)} peut être la suivante :
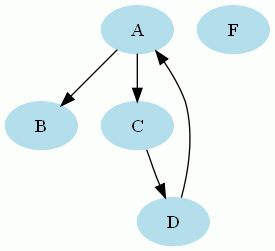
Formellement, un graphe non orienté est un couple (S, A) où S est l'ensemble des sommets du graphe et A est l'ensemble des arêtes du graphe. Chaque arête est un couple de sommets non ordonnés (ou un ensemble de deux éléments) dont les deux éléments relient deux sommets du graphe indépendamment de son orientation.
Par exemple, une représentation graphique du graphe non orienté G = (S,A), avec S = {A,B,C,D,E,F,H} et A={{A,B}, {A,C}, {C,F}, {B,D}, {D,E}, {D,H}} est la suivante :
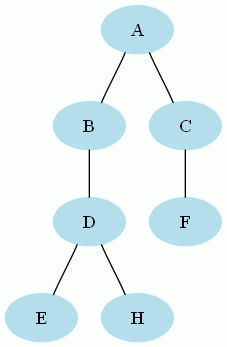
On appelle un arc (dans un graphe orienté) ou arête (dans un graphe non orienté) ce qui relie deux sommets (ou nœuds).
Un algorithme de plus court chemin permet de trouver un ou des chemins ayant le plus faible poids dans un graphe pondéré, c'est-à-dire que la somme des poids des arcs/arêtes du chemin trouvé est la plus faible possible. On peut distinguer principalement trois variantes de l'algorithme :
- plus court chemin à origine unique. Il s'agit ici de calculer l'ensemble des plus courts chemins entre un sommet de départ et l'ensemble des sommets du graphe. On peut aussi être amené à calculer les plus courts chemins à destination unique, mais il s'agit en fait du même problème ;
- plus court chemin pour un couple de sommets. Le but est de calculer le plus court chemin entre un sommet de départ et un sommet d'arrivée ;
- plus court chemin pour tous couples de sommets. L'idée est ici d'obtenir le même résultat que précédemment, mais pour l'ensemble des couples du graphe.
Dans un graphe non orienté, une boucle est une arête dont les deux extrémités sont le même sommet.
Par exemple, le graphe suivant :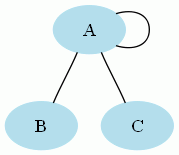
admet une unique boucle sur le sommet A.
On parle de chemin pour les graphes orientés et on parle de chaîne pour les graphes non orientés, mais ces termes admettent des définitions relativement proches.
Dans un graphe orienté, un chemin est une séquence (s_1, a_1, s_2, a_2... s_n) (où pour tout i (de 1 à n), s_i est un sommet du graphe et a_i est un arc du graphe) allant du sommet s_i au sommet s_{i+1}. Par exemple, dans :
le chemin (A, (A,C), C, (C, D), D) est un chemin allant de A à D.
De manière équivalente, dans un graphe non orienté, une chaîne est une séquence (s_1, a_1, s_2, a_2... s_n) (où pour tout i (de 1 à n), s_i est un sommet du graphe et a_i est une arête du graphe) admettant les sommets s_i et s_{i+1} comme extrémités. Par exemple, dans le graphe suivant :
la séquence (A, {A,B}, B, {B,D}, D} est une chaîne allant du sommet A au sommet D.
En revanche, la séquence (A, {A,B}, B, {B,C}, C} n'est pas une chaîne, car l'arête {B,C} n'appartient pas au graphe.
À noter que dans la littérature sur les graphes, on utilise parfois seulement le terme chemin, pour parler à la fois des chemins et des chaînes.
Qu'est-ce qu'un graphe connexe/fortement connexe ?
Un graphe connexe (resp. fortement connexe) est un graphe non orienté (resp. orienté) si et seulement si pour tous couples de sommets du graphe (s1, s2), il existe une chaîne (resp. un chemin) entre s1 et s2.
Exemples
Graphe connexe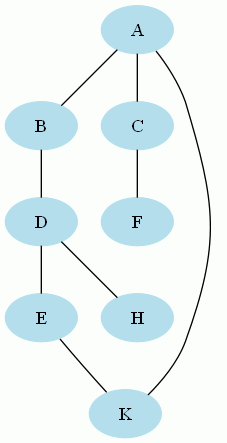
Graphe non connexe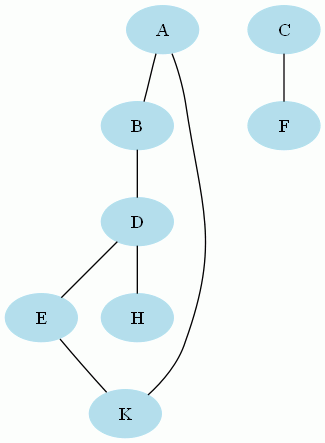
Graphe non fortement connexe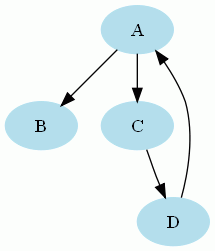
Graphe fortement connexe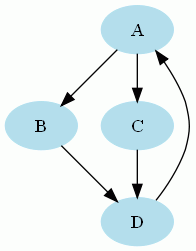
Le terme cycle est utilisé pour les graphes non orientés et le terme circuit est utilisé pour les graphes orientés mais disposent de définitions proches.
Un cycle (resp. un circuit) est un chemin (resp. une chaîne) admettant le même sommet comme sommet de départ et comme sommet d'arrivée.
Dans le graphe orienté suivant :
le chemin (A, (A,C),C, (C,D),D,(D,A),A) est un cycle. En revanche, le chemin : (A, (A,C),C, (C,D),D,(D,A),A, (A,C), C) n'est pas un cycle, le sommet initial A ne correspond pas au sommet final C.
Un arbre est un graphe non orienté connexe sans cycle.
Exemples
Le graphe suivant est un arbre :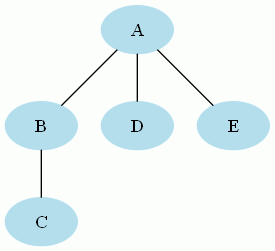
Le graphe suivant admettant le cycle (A,C,D,A) n'est pas un arbre :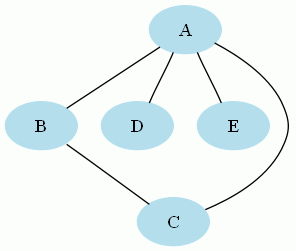
Le graphe suivant bien que n'admettant pas de cycle est non connexe (ce n'est donc pas un arbre) :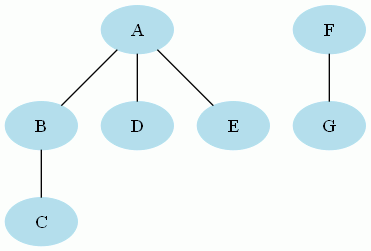
Une forêt est un graphe sans cycle. Chaque composante connexe d'une forêt est donc un arbre.
Ceci est une forêt :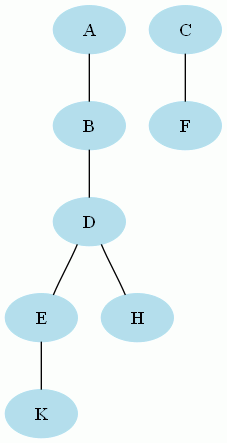
Ceci n'en est pas une étant donné que le sous-graphe à gauche admet des cycles :
Un graphe G' = (S', A') est appelé sous-graphe d'un graphe G = (S,A) si et seulement si S' est inclus dans S et A' est inclus dans A.
Dans le cas où les sommets des deux graphes sont identiques (S = S'), G' est appelé graphe couvrant ou sous-graphe couvrant ou graphe partiel de G.
Exemple avec : G = ( {1,2,3}, {{1,2}, {2,3}} :
- le graphe G' = ( {1,2}, {{1,2}} ) est un sous-graphe de G ;
- le graphe ( {1,2,3}, {{1,2}} ) est un graphe couvrant de G.
En revanche : B = ( {1,2}, {{1,2}, {1,3}} ) n'est pas un sous-graphe de G, car B n'est pas un graphe du tout.
Dans un graphe non orienté, le voisinage d'un nœud est l'ensemble des voisins de ce nœud sachant que le voisin d'un nœud est lui-même un nœud qui est relié à un autre par le biais d'une arête. Dans un graphe orienté, on a deux types de voisinage, le voisinage interne (par les arcs qui arrivent à ce nœud) et le voisinage externe (par les arcs qui partent de ce nœud).
Ce célèbre problème peut se résumer de la façon suivante : dans la ville de Köenigsberg il existe sept ponts : peut-on traverser tous les ponts une et seulement une seule fois pour revenir à son point de départ ? C'est aussi un problème considéré comme la toute première application liée aux graphes, qui a été introduit et résolu par Euler. Le problème peut donc se résoudre en essayant de trouver un graphe eulérien, ce qui n'est pas possible.
Un graphe complet est un graphe dont les sommets sont tous reliés deux à deux par une arête.
Un graphe planaire est un graphe admettant au moins une représentation graphique planaire sans qu'aucune arête ne se croise.
On associe souvent la notion de graphe planaire au théorème des quatre couleurs.
Graphe planaire (on peut le dessiner sur un plan sans qu'aucune arête ne se croise) :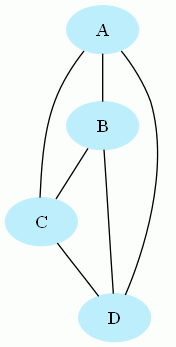
Graphe non planaire (il n'est pas possible de dessiner ce graphe sans qu'aucune arête ne se croise) :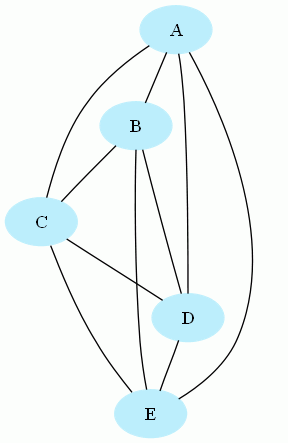
Une clique est un sous-graphe complet, il s'agit donc du complémentaire du stable. La recherche de la clique maximale (ie: qui contient le plus de sommets possible) peut servir à d'autres problèmes de la théorie des graphes. En effet, la cardinalité de la clique maximale est un minorant du nombre chromatique.
Une k-clique est une clique de cardinalité k, c'est-à-dire qu'elle contient k sommets.
Un stable est un sous-graphe qui ne contient que des sommets deux à deux non adjacents. De par cette définition, il s'agit du complémentaire d'une clique. Comme le stable n'est souvent pas unique, il existe le problème de la recherche du stable maximum dans un graphe. C'est-à-dire du stable possédant le plus grand nombre de sommets.
Un graphe eulérien est un graphe qui admet un parcours eulérien, c'est-à-dire que le graphe peut être parcouru en passant une et une seule fois par chaque arête. L'application la plus connue est avec les ponts de Köenigsberg d'où le nom.
Un graphe hamiltonien est un graphe qui admet une chaîne hamiltonienne, c'est-à-dire que le graphe peut être parcouru en passant une et seulement une seule fois par chaque sommet.
Un parcours de graphe est un algorithme qui permet de déterminer la descendance d'un sommet S. On entend par descendance l'ensemble des sommets tels qu'il existe un chemin de S vers l'un de ces sommets.
Les algorithmes de parcours les plus connus sont le parcours en largeur et le parcours en profondeur.
Dans le parcours en largeur, les sommets sont visités par ordre de distance vers le sommet d'origine S. Dans un premier temps, ce sont les sommets se trouvant à une distance 1 de S qui sont visités, puis à une distance 2 jusqu'à ce qu'il ne reste plus de sommets à visiter.
Dans le parcours en profondeur, on descend en profondeur dans le graphe jusqu'à ce qu'il n'y ait plus de sommet à visiter, puis on revient aux sommets parents pour continuer le processus.
Un graphe A est un arbre couvrant d'un graphe non orienté G si et seulement si A est un arbre et A est un sous-graphe couvrant de G.
L'arbre A = ({A,B,C,D,E,F}, {{A,B}, {B,C}, {D,E}, {A,E}, {A,F} }) (en rouge) est un arbre couvrant du graphe entier.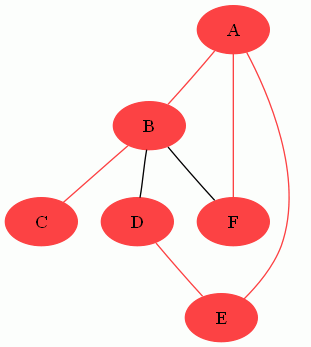
Ce problème peut se résumer de la façon suivante : un commercial doit vendre son produit dans plusieurs endroits et il doit se trouver un chemin qui ne passe qu'une seule fois par chaque ville pour revenir à son point de départ. Ce problème revient donc à chercher un cycle hamiltonien dans un graphe. N'hésitez pas à consulter les deux articles mentionnés ci-dessous.
Ce problème peut être résumé de la façon suivante : la coloration d'un graphe consiste à donner une couleur à tous les sommets, de telles manières que deux sommets voisins (reliés par un arc ou une arête) ne possèdent pas la même couleur.
Le nombre chromatique d'un graphe est le plus petit nombre de couleurs distinctes suffisant à colorer ce graphe.
L'ordre d'un graphe est le nombre de sommets de ce graphe.
Un graphe est dit biparti si et seulement s'il existe une répartition des sommets de ce graphe en deux sous-ensembles tels que toutes les arêtes du graphe ont un sommet dans chacun des deux sous-ensembles.
Dans le cas d'un graphe orienté, l'arité d'un nœud correspond au nombre d'arcs sortant du nœud, il s'agit donc du degré extérieur (ou sortant) du nœud. Dans le cas particulier d'un arbre, l'arité correspond au nombre de ses fils.
On appelle degré d'un nœud, le nombre de ses arêtes adjacentes. Dans le cas d'un graphe orienté, on peut distinguer le degré extérieur (ou entrant) du degré intérieur (ou entrant) qui sont respectivement le nombre de ses arêtes incidentes et sortantes.
Le degré d'un graphe est le maximum des degrés de ses sommets. Dans un graphe orienté cela correspond donc au maximum de l'arité de ses sommets.
Par dualité avec le voisinage de sommets, on dit que deux arêtes sont incidentes si elles ont un sommet en commun.
Le carré d'un graphe G est le graphe G' qui a les mêmes sommets que G et dont deux sommets sont reliés, s'ils sont reliés dans le graphe G d'origine ou s'ils ont un voisin en commun dans G.
Un puits est un sommet d'un graphe orienté dont le degré sortant est égal à 0.
Une source est un sommet d'un graphe orienté dont le degré entrant est égal à 0.
Un sommet pendant est un sommet de degré 1.
Un ensemble dominant est un sous-ensemble de sommets d'un graphe, tel que chaque sommet du graphe est soit dans l'ensemble dominant, soit voisin d'un sommet de l'ensemble dominant.
Un graphe acyclique est un graphe qui ne contient aucun cycle.
Une partition des sommets d'un graphe est une famille disjointe d'ensembles de sommets tels que leur union est l'ensemble de tous les sommets.
Une valuation de graphe est une fonction qui associe un réel à chaque arête.
Un graphe régulier est un graphe dans lequel tous les sommets ont le même degré. Si tous les sommets sont de degré k alors on parle de graphe k-régulier.
Un graphe cubique est un graphe 3-régulier.
Admettons que A soit un sous-ensemble d'un graphe G, et R une relation d'ordre sur G. Un majorant (resp. minorant) de A est un élément M (resp. m) dans G tel que : pour tout x appartenant à A on a xRM (resp. mRx).
Admettons que A soit un sous-ensemble d'un graphe G, et R une relation d'ordre sur G. Le maximum (resp.minimum) de A, s'il existe, est l'unique élément M (resp. m) dans A qui vérifie : pour tout x appartenant à A on a xRM (resp. mRx).
Admettons que A soit un sous-ensemble d'un graphe G, et R une relation d'ordre sur G. La borne supérieure (resp. inférieure) de A, si elle existe, est le plus petit (resp. grand) des majorants (resp. minorants). Tout ceci suivant bien sûr la relation d'ordre R.
Admettons que A soit un sous-ensemble d'un graphe G, et R une relation d'ordre sur G. Un élément maximal (resp. minimal) est un élément de A qui n'a pas de majorant (resp. minorant) dans A.
Dans un graphe une relation d'ordre est aussi une relation binaire, c'est-à-dire que chaque sommet de ce graphe est ordonné de manière cohérente suivant une règle précise.
Proposer une nouvelle réponse sur la FAQ
Ce n'est pas l'endroit pour poser des questions, allez plutôt sur le forum de la rubrique pour çaLes sources présentées sur cette page sont libres de droits et vous pouvez les utiliser à votre convenance. Par contre, la page de présentation constitue une œuvre intellectuelle protégée par les droits d'auteur. Copyright © 2026 Developpez Developpez LLC. Tous droits réservés Developpez LLC. Aucune reproduction, même partielle, ne peut être faite de ce site et de l'ensemble de son contenu : textes, documents et images sans l'autorisation expresse de Developpez LLC. Sinon vous encourez selon la loi jusqu'à trois ans de prison et jusqu'à 300 000 € de dommages et intérêts.




