CPLEX est une solution logicielle d'IBM pour la résolution de problèmes d'optimisation mathématique et de problèmes de résolution de contraintes. Cette année, lors de la réunion annuelle de l'INFORMS, une société professionnelle pour la recherche opérationnelle (OR) et les sciences de gestion (MS), les développeurs de CPLEX sont revenus sur une série de nouveautés qui devraient faire leur apparition dans la version 12.10 — normalement, en décembre-janvier, comme chaque année. L'un des grands mots clés de cette version sera l'apprentissage automatique, qu'il soit supervisé ou par renforcement.[h=2]Apprentissage par renforcement et programmation par contraintes[/h]
Le moteur de programmation par contraintes devrait voir sa performance largement améliorée pour les problèmes de réalisabilité, c'est-à-dire pour trouver une solution qui satisfait toutes les contraintes. Les évolutions ont déjà été intéressantes pour ces dernières versions, avec un temps de résolution qui baisse d'un facteur de presque 3,5 sur cinq ans. D'un point de vue algorithmique, il s'agit surtout d'un algorithme d'exploration : la plongée itérative, qui peut plonger très vite dans l'arbre sans effectuer trop de propagations à chaque nœud.
Cette nouvelle version apportera une technique d'apprentissage par renforcement pour choisir la meilleure stratégie de recherche et de propagation dans l'arbre. De manière automatique, désormais, CP Optimizer choisira la meilleure stratégie parmi toutes celles disponibles pour le problème à résoudre, en s'adaptant à l'aide d'apprentissage par renforcement. De manière générale, cette technique divise les temps de calcul par 1,5, mais les résultats sont plus impressionnants pour les problèmes de réalisabilité.
Plus de détails dans la présentation idoine.
[h=2]Apprentissage supervisé et linéarisation de MIQP[/h]
Les problèmes en nombres entiers quadratiques convexes peuvent se résoudre de différentes manières quand les produits ne se font qu'entre variables binaires (ou une variable binaire et une variable continue). On peut reformuler le produit z = xy en trois contraintes : x <= y, z <= y, z >= x + y - 1. Depuis CPLEX 12.5, en 2012, le solveur peut automatiquement effectuer cette réécriture pour linéariser le problème et retomber sur une classe mieux connue : les problèmes linéaires en nombres entiers. Jusque CPLEX 12.9, il s'agit d'ailleurs de la technique par défaut.
Sauf que… la linéarisation n'est pas toujours le meilleur choix. Selon les problèmes, il vaut mieux parfois aborder le problème avec son objectif quadratique. De fait, la reformulation ajoute une variable binaire par produit, ainsi que trois contraintes… Ainsi, des chercheurs travaillant sur CPLEX ont d'abord construit un classificateur qui détermine s'il vaut mieux appliquer cette reformulation ou pas (si elle a une chance de diminuer le temps de résolution d'au moins dix pour cent). Ils ont commencé par construire une base de données de problèmes MIQP pour récupérer assez de données, puis ont construit un classificateur utilisant 77 variables (caractéristiques du problème ou de sa résolution à un moment donné).
Cette approche ne pouvait cependant pas fonctionner en pratique : parmi les variables utilisées pour l'entraînement des modèles d'apprentissage, il y avait les ordres de grandeur des valeurs propres du terme quadratique dans l'objectif. Cependant, CPLEX n'utilise jamais cette information dans son processus de résolution : il aurait fallu les calculer, ce qui double le temps de résolution du nœud racine (problème relâché, sans contraintes d'intégrité). En s'aidant du calcul d'importance des variables, ils se sont limités à 21 variables. La variable la plus importante initialement n'étant pas calculable rapidement (valeur du nœud racine avec et sans reformulation), ils ont construit un modèle de régression pour l'estimer. Le meilleur modèle entraîné est ainsi passé d'une forêt aléatoire (sur les 77 variables) à une SVM, déployée dans CPLEX 12.10.
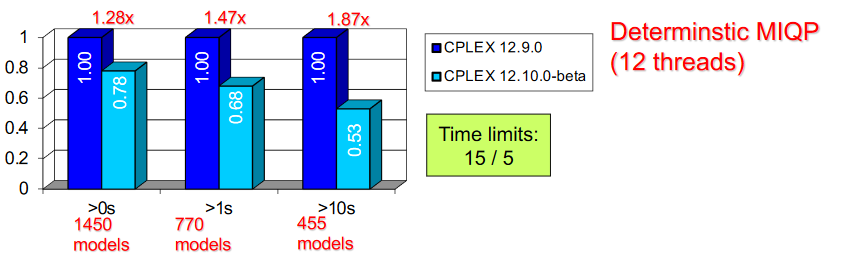
Plus de détails dans la présentation idoine.
[h=2]Système de fonctions de rappel génériques[/h]
Le gros apport de CPLEX 12.8 était un nouveau système de fonctions de rappel, le principal défaut du système précédent était de changer complètement le comportement du solveur selon que des fonctions de rappel sont utilisées ou non (y compris quand ces fonctions ne font rien…). Ce nouveau système est bien plus simple et plus facile à étendre. À terme, il devrait permettre plus de contrôle sur le processus de recherche. Cette refonte rend le système bien plus flexible, plus facile à expliquer, mais au détriment d'une certaine facilité d'utilisation : CPLEX ne cherche pas à cacher son utilisation de plusieurs fils d'exécution (le système précédent datant des années 1990, cette subtilité n'était pas prise en compte). En particulier, cela signifie que l'utilisateur n'a plus qu'un seul type de fonction disponible (mais avec un contexte particulier : dès qu'une solution au problème relâché ou une solution entière est trouvée, par exemple) et n'a plus accès au modèle après prétraitement.
Le système apporté dans CPLEX 12.8 était un peu rudimentaire, toutes les fonctionnalités nécessaires n'étant pas forcément disponibles. Avec CPLEX 12.9, il est devenu possible de récupérer l'état global de la résolution dans des problèmes distribués ; l'utilisateur peut aussi désormais injecter des solutions heuristiques de manière plus flexible. CPLEX 12.10 apportera la possibilité de récupérer plus d'informations, mais aussi d'influencer les décisions de branchement.
Plus de détails dans la présentation idoine.
[h=2]Améliorations de performance incrémentales[/h]
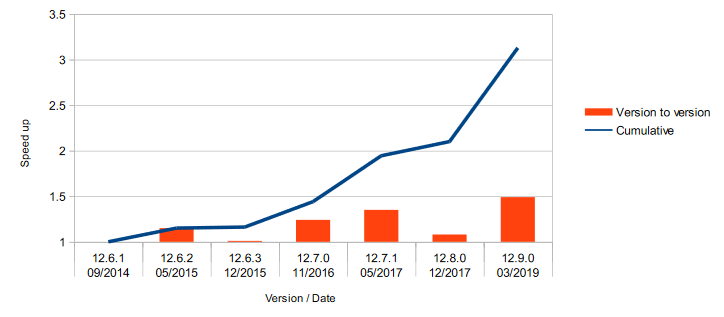
Comme à chaque version, tous les composants de CPLEX ont été améliorés pour extraire encore un peu plus de performance. Par exemple, le solveur de problèmes linéaires continus a été partiellement retravaillé pour mieux exploiter les instructions SIMD des processeurs modernes, en plus d'une mise à jour du compilateur. D'un point de vue algorithmique, les variables superbasiques (variables hors base qui atteignent l'une de leurs bornes) sont mieux gérées dans la procédure de métissage (qui permet de passer de la solution d'un algorithme de point intérieur à un point extrême du polytope). Le solveur parallèle effectue de meilleurs prétraitements sur la formulation qui lui est donnée.
Pour les problèmes linéaires en nombres entiers, l'amélioration de performance est légèrement plus élevée. Ceci est dû à une recherche dynamique améliorée dans les cas où elle doit redémarrer (7 % des modèles de test sont affectés, avec une réduction moyenne de 12 % des temps de calcul), mais aussi à une meilleure implémentation des variables indicatrices (très peu de modèles impactés, mais avec 20 % de réduction de temps de calcul pour ceux-ci). De nouvelles heuristiques expliquent un à deux pour cent de l'amélioration globale. Le reste provient d'améliorations dans la génération de plans sécants : la résolution du problème de séparation des coupes {0, 1/2} pour les contraintes denses en variables binaires (5 % de modèles affectés, 10 % de réduction), l'exploitation des nœuds explorés et irréalisables à l'aide de coupes de Farkas (2 % de réduction des temps de calcul pour tous les modèles).
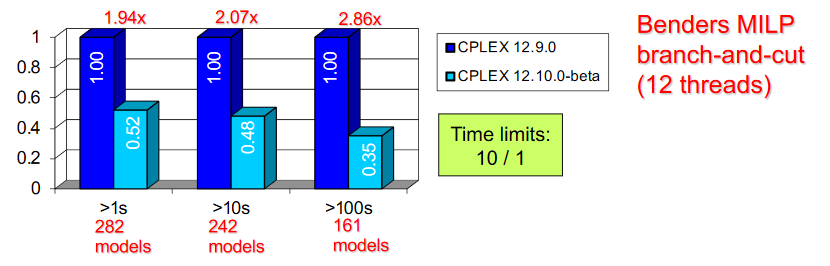
La décomposition de Benders est un algorithme relativement neuf dans CPLEX, arrivé seulement dans la version 12.7 (en 2017). Les améliorations sont cependant intéressantes : une accélération qui peut monter à un facteur 2,86 (réduction de temps de calcul) pour les modèles qui prenaient auparavant plus de cent secondes à résoudre (uniquement sur un jeu de problèmes de test spécifique à la décomposition de Benders, composé principalement de programmes stochastiques en nombres entiers — 209 sur un total de 375). Un meilleur prétraitement de la formulation d'entrée explique deux pour cent de l'amélioration, une gestion plus proactive des plans sécants générés participe pour autant au résultat complet. D'un point de vue plus fondamental, la grosse nouveauté est l'implémentation des GBC (general bound constraint) : à elle seule, cette modification explique cinq pour cent de la réduction de temps globale… mais apporte un facteur 66 pour certains problèmes !
Plus de détails dans la présentation idoine.
Sources et images : présentations.