Recherche opérationnelle : CPLEX 12.7 apporte une décomposition de Benders automatique

Les temps de résolution réduits d'un facteur jusque dix

CPLEX est l’un des plus vieux solveurs d’optimisation à ce jour… et parmi les plus performants. Malgré son héritage (il est commercialisé depuis 1988 !), la nouvelle version, numérotée 12.7 et disponible depuis le 11 novembre, apporte de nouvelles améliorations de performance (tout comme les concurrents Gurobi et MOSEK, c’est habituel), mais ce n’est pas tout : outre des facilités de modélisation (comme Gurobi, CPLEX 12.7 permet d’effectuer une décomposition de Benders de manière (semi-)automatique.

Performance

Les améliorations de performance principales se situent au niveau des MILP — problèmes linéaires en nombres entiers — (voir figure) : 7 % au niveau de la résolution du LP, 15 % pour des MILP compliqués. Les MIQP (problèmes quadratiques en nombres entiers) voient eux aussi une amélioration de l’ordre de 15 % pour les problèmes les plus difficiles, tandis que les MIQCP ont même une amélioration de 22 % sur des problèmes difficiles.


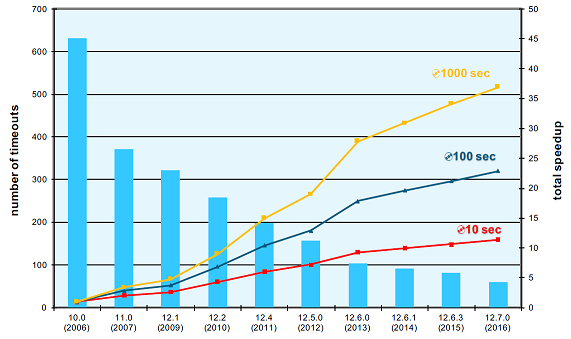
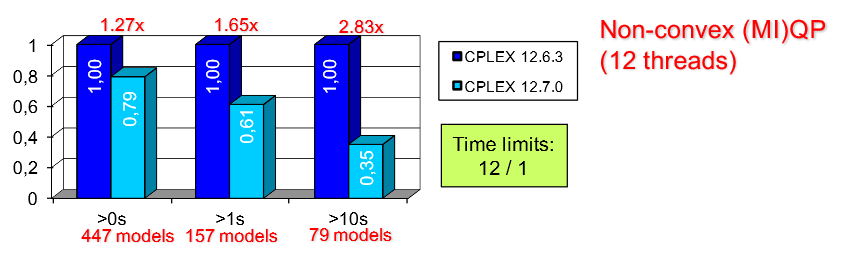
Cependant, l’amélioration la plus spectaculaire vient des problèmes quadratiques (MIQP) non convexes : les modèles les plus difficiles prennent 65 % de temps en moins ! Pour les autres catégories de problèmes, quand on ignore le fait que certaines variables soient entières, on peut trouver la solution optimale en des temps raisonnables ; dans le cas non convexe, cette propriété n’est plus vérifiée et trouver la solution optimale en variables continues est déjà un challenge en soi. L’amélioration provient des plans sécants par reformulation-linéarisation.


Décomposition de Benders

Certains problèmes ont une structure décomposable, c’est-à-dire qu’on peut les résoudre par blocs relativement indépendants. Par exemple, dans un problème stochastique, on prend une série de décisions que l’on évalue dans une série de situations : ces évaluations sont indépendantes les unes des autres. Dans ce genre de cas (et bien d’autres), une décomposition de Benders peut s’appliquer : les décisions principales correspondront à un nœud racine, les évaluations à des sous-problèmes.

Cependant, cette décomposition est loin d’être facile à implémenter — il faut appliquer la théorie de la dualité pour faire passer l’information des sous-problèmes à la racine et vice-versa. Cette nouvelle version de CPLEX propose d’automatiser en grande partie cette étape, selon plusieurs modes d’opération : laisser CPLEX s’occuper entièrement de la décomposition (choisir les variables du problème racine et des sous-problèmes), proposer soi-même une première décomposition et laisser CPLEX la retravailler (diviser les sous-problèmes), entièrement spécifier la décomposition.

Selon les types de problème, cette décomposition automatique peut apporter un certain bénéfice ou pas : pour le jeu de tests habituel de CPLEX, cinq pour cent des problèmes prenant plus de dix secondes de calcul voient une amélioration. Par contre, sur des problèmes où la décomposition de Benders est bien mieux adaptée, les effets sont plus visibles : une résolution trois fois plus rapide sur tous les problèmes du jeu de tests spécifique, dix fois plus pour les plus ardus (temps de résolution supérieur à cent secondes).

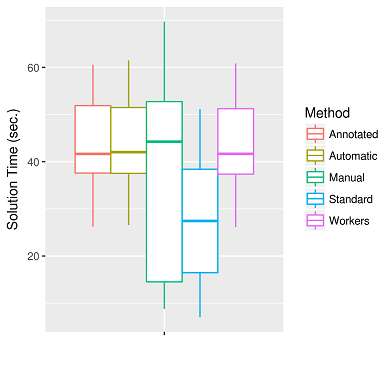
D’après des tests indépendants, cette fonctionnalité fonctionne très bien : elle n’est pas plus lente qu’une implémentation manuelle, même en laissant CPLEX choisir la meilleure manière d’effectuer la décomposition (au niveau des temps de démarrage, avant le début de la résolution du problème, apporter des annotations semble néfaste). Ainsi, pour la plupart des utilisateurs, rien ne justifie vraiment l’investissement dans une implémentation de cette décomposition : le solveur le fait très bien lui-même.


Aides à la modélisation

Écrire des programmes d’optimisation complexes n’est pas forcément une mince affaire, CPLEX propose de prémâcher une partie du travail. Notamment, un nouveau paramètre demande au solveur d’analyser le problème et de proposer des améliorations — par exemple, remplacer des contraintes avec des constantes assez grandes (“big-M”) par des contraintes indicatrices.

Cette fonctionnalité vient compléter l’analyse de la dégénérescence lors des calculs. La dernière version propose également d’analyser, de manière automatique, la variabilité de performance — ce qui indique probablement quelques problèmes dans la modélisation.

La modélisation des fonctions linéaires par morceau est maintenant accessible tant en C et Python que dans les fichiers LP (c’était déjà le cas en C++, C# et Java).

Sources et images : Recent advances in IBM ILOG CPLEX @INFORMS 2016, What’s in CPLEX Optimization Studio 12.7?, IBM CPLEX Optimization Studio 12.7 – Benders, Modeling Assistance, etc.