I. Introduction▲
Les arbres informatiques sont parmi les plus utiles -- et les plus fascinantes -- structures de données évoluées que l'on puisse manipuler. Les arbres sont utiles pour modéliser et éventuellement faire persister des données aussi différentes, par exemple, que :
- la décomposition en pièces ou en « composants » d'un objet industriel aussi complexe que l'aile d'un avion Boeing 747, soit plusieurs millions de pièces ;
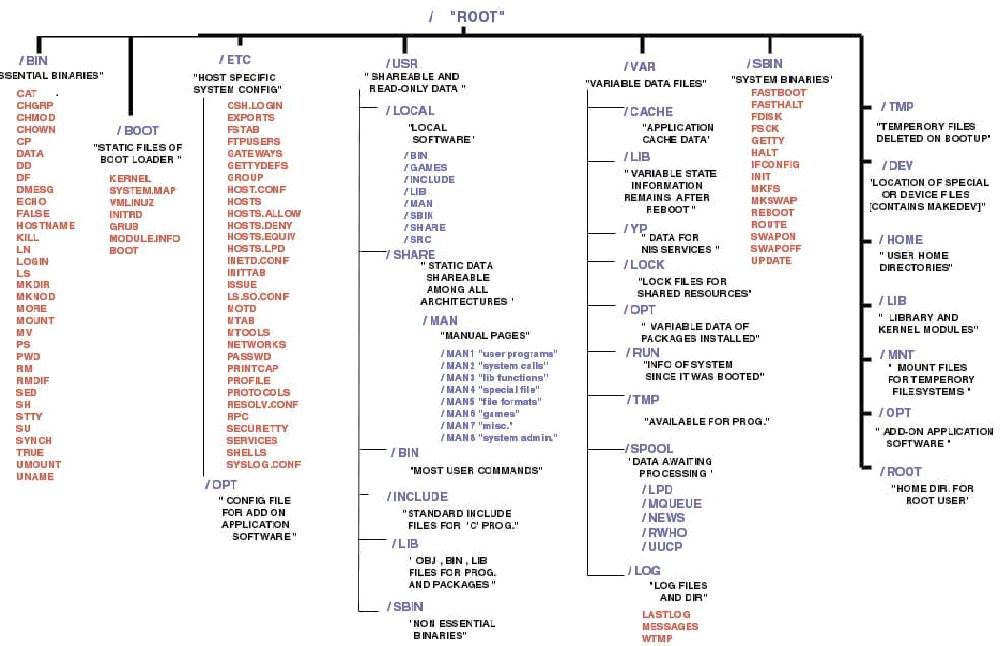
- la structure d'un système de gestion de fichiers du type Unix, dont on a un bel exemple grâce à Wikipédia, est reproduite sur la page suivante ;
- l'arbre généalogique de votre famille sur une longue période ;
- une recette gastronomique de la cuisine française faisant appel à des « sous-recettes » ou une formule chimique, par exemple un plat classique à sauce du répertoire d'Auguste Escoffier :Volaille->Garniture->Accompagnement->Sauce->…
On devrait se poser de suite la question principale : « Qu'est-ce qu'un nœud dans un arbre informatique ? » La réponse est simple : c'est un objet appartenant à l'arbre, parce qu'il possède quatre propriétés : un Niveau, un Rang, et un Père (parfois dénommé « propriétaire » ou bien « ascendant ») ; il possède également, bien sûr, une Valeur.
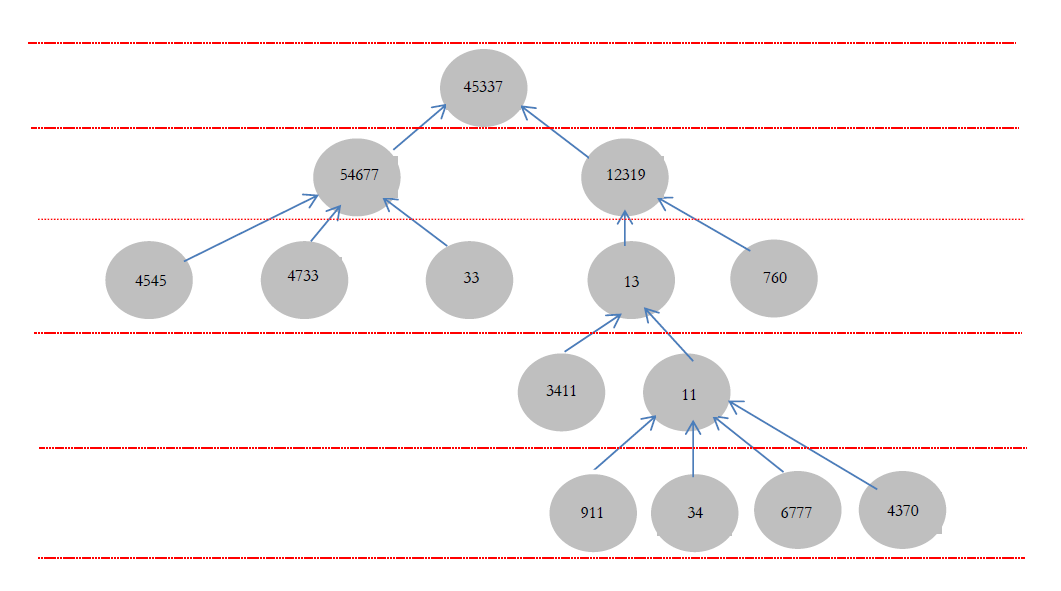
Examinons l'exemple d'arbre simple suivant à seulement cinq niveaux :
Pour bien comprendre le code C#, on peut commencer par matérialiser cet exemple d'arbre à quatorze nœuds à travers les données du tableau suivant, qui réalise la transformation « arbre » vers « tableau » :
|
Niveau |
Rang |
Propriétaire |
Valeur |
Remarques |
|
1 |
1 |
0 |
45337 |
Tête de l'Arbre : pas de propriétaire |
|
2 |
1 |
1 |
54677 |
|
|
2 |
2 |
1 |
12319 |
Nœud Intermédiaire : a des dépendants |
|
3 |
1 |
1 |
4545 |
|
|
3 |
2 |
1 |
4733 |
|
|
3 |
3 |
1 |
33 |
Nœud Feuille sur son niveau |
|
3 |
4 |
2 |
13 |
|
|
3 |
5 |
2 |
760 |
|
|
4 |
1 |
4 |
3411 |
|
|
4 |
2 |
4 |
11 |
|
|
5 |
1 |
2 |
911 |
Nœud Feuille au niveau le plus profond |
|
5 |
2 |
2 |
34 |
Nœud Feuille au niveau le plus profond |
|
5 |
3 |
2 |
6777 |
Nœud Feuille au niveau le plus profond |
|
5 |
4 |
2 |
4370 |
Nœud Feuille au niveau le plus profond |
|
5 |
4 |
2 |
4370 |
Doublon : Erreur |
|
4 |
1 |
4 |
4901 |
Adresse (N,R) en Doublon : Erreur |
Il est très important de comprendre que les deux dernières lignes de ce tableau vont provoquer des erreurs : l'une parce que la ligne est dupliquée (interdite), l'autre parce que l'adresse « 4 1 » existe déjà, également interdite.
À strictement parler, l'arbre n'est pas une structure de données générique simple au même type que la Liste, la Table de Hachage ou le Dictionnaire, par exemple : c'est plutôt une « superstructure » des données, faisant appel à certaines structures de données génériques : la preuve, c'est que ni le STL C++ ni les génériques C# n'en contiennent. Notre solution utilise intensément les « List » et les Templates.
Pour reprendre l'exemple de l'aile d'un avion Boeing 747, seule une gestion arborescente permet de répondre à des questions du type : si la « pièce » XYZ n'est pas en stock aujourd'hui, quels sont les composants que je ne peux pas fabriquer ou assembler, car embarquant cette même pièce ?
Dans le monde réel, l'information qui décrit les caractéristiques du nœud (la pièce dans notre exemple) résidera quasi systématiquement dans une table référentielle d'une base de données : à vous d'instancier et gérer l'arbre hiérarchique des dépendances et relations entre pièces.
Notons que le Microsoft CLR (Common Language Runtime) contient un objet de type « TreeView », mais il ne s'agit pas ici d'une bibliothèque facilitant l'affichage des arbres dans des pages WEB ou dans Windows Forms‑: il s'agit d'une bibliothèque extensible de bas niveau permettant de manipuler des arbres en mémoire indépendamment de leur présentation à l'utilisateur.
Une des caractéristiques les plus saisissantes de l'arbre, c'est qu'à la différence d'autres structures de données évoluées du type « liste dichotomique » ou liste à clef de hachage, les arbres existent dans la nature, tels quels, et nous n'avons qu'à nous en inspirer.
C'est à double titre que les arbres nous intéressent : aussi bien les branches et les feuilles (la partie visible) que la partie cachée et invisible consistant en racines et nodules, nous inspirent.
Ce qui nous frappe d'emblée lors que nous examinons un arbre centenaire, c'est que nous ne voyons pas combien de branches et de feuilles il contient, et c'est là la première contrainte d'une bonne implémentation d'un arbre : on doit pouvoir modéliser un arbre de complexité très grande, dont nous ne connaissons ni le nombre de « branches » (les « niveaux »), ni le nombre de feuilles de la branche.
Dans l'implémentation C#/.Net que j'ai confectionnée, les contraintes habituelles de l'arbre sont respectées à la lettre, c'est-à-dire :
- nous modélisons un arbre de profondeur arbitraire ; en réalité, le nombre de nœuds dans l'arbre n'est limité que par le nombre d'éléments que l'on puisse stocker dans un objet de type Liste<T> via les génériques, soit un nombre très grand ;
- l'arbre est générique, c'est-à-dire que la valeur stockée dans chaque nœud de l'arbre est faiblement typée, de telle manière qu'il puisse stocker, soit une chaîne de caractères par exemple, « AX1233CXCT22244 », une des pièces (un vérin poussoir, en l'occurrence) entrant dans la composition de notre aile d'avion Boeing cité plus haut, soit un entier du type « 349422339 », la clef numérique d'une pièce référencée dans le référentiel d'une base de données ;
- la valeur de la clef n'est pas unique : dans un arbre, la clef peut figurer à différents endroits d'un arbre, et l'arbre est faiblement typé ;
-
les contraintes purement techniques et « formelles » sont implémentées, ce qui veut dire que :
- chaque nœud n'est rattaché qu'à un seul et unique père-propriétaire au niveau immédiatement supérieur,
- l'intégrité physique de l'arbre est préservée, c'est-à-dire qu'il n'y a pas d'orphelins (nœuds sans père), ni de suppression d'un nœud tant qu'il a des nœuds dépendants,
- chaque arbre a un seul nœud « tête ».
Notons que dans notre implémentation l'ordre d'insertion des nœuds n'est pas imposé, avec comme corollaire qu'un parcours séquentiel de la liste ne donne aucune information vraiment utile sur l'arborescence au sens strict, bien qu'il donne des informations importantes sur les valeurs stockées individuellement dans l'arbre.
Qui plus est, l'intégrité de l'arbre est garantie à tout moment, lors des insertions et suppressions ; si ceci n'était pas le cas, on devrait déléguer aux méthodes de parcours de l'arbre une détection d'anomalie dans la structure arborescente, une véritable « boîte de Pandore » qui accroît la complexité.
- Toutes les opérations classiques (insertion, suppression, modification) sont supportées, en respectant les contraintes de l'intégrité physique et logique notées ci-dessus ; c'est donc un choix « ceinture et bretelles », car les méthodes d'accès s'appuient sur le fait que l'arbre est intègre vis-à-vis des accesseurs.
II. L'Implémentation▲
Notre implémentation s'appuie essentiellement sur une structure C#/.Net du type :
List<Tree<T>.TreeNode>Nous utilisons donc une Liste contenant des « structures anonymes » de type TreeNode, dont la clef est un template T. Bien qu'il y ait beaucoup d'autres structures adaptables, ce type est particulièrement performant, car sa caractéristique principale, c'est qu'il est très performant pour la gestion d'arbres de grande taille faisant l'objet d'insertions et modifications importantes, car le coût d'une insertion/modification/suppression, c'est le coût d'un Objet.Add(…) élémentaire C#, soit un coût très faible.
Ceux qui connaissent bien les arbres remarqueront que mon objectif n'a pas été de gérer un « B-Tree », dont la propriété principale est l'équilibre binaire de l'arbre : chaque « niveau » de l'arbre n'a que deux et seulement deux nœuds, de manière à ce que l'accès en lecture via une recherche dite dichotomique soit excessivement rapide est déterministe, donnée par la célèbre formule :
kitxmlcodelatexdvpNombre\_De\_ Recherches = O\left ( log_{b}n \right ) op\'erationsfinkitxmlcodelatexdvpBien qu'exceptionnellement utiles dans certains cas d'analyse, les « Balanced Binary Tree » (arbre binaire équilibré) ont souvent un coût très élevé de mise à jour : l'insertion d'un nouveau nœud peut entraîner la réorganisation complète de l'arbre.
Notre approche est à la fois plus intuitive et plus pragmatique : nous nous basons sur une pile (« stack » en anglais), en nous contentant « d'empiler » de nouveaux nœuds dessus, sans nous occuper de l'ordre d'empilement.
Toutes les méthodes habituelles pour parcourir l'arbre sont implémentées, soit de « haut en bas » via une méthode du type :
List<Tree<T>.TreeNode> traverseByAddressFull()soit « de bas en haut », via une méthode du type :
List<Tree<T>.TreeNode> ascendByAddress()C'est le « Saint Graal » de la gestion des arbres : parcourir l'arbre dans n'importe quel sens, à partir de n'importe quel endroit, simplement en fournissant, soit son adresse (Niveau,Rang,Propriétaire,Valeur), soit en fournissant sa valeur de clef de type T, par exemple : « 349422339 », tout en s'assurant du respect des contraintes d'intégrité.
Nous remarquerons dans la littérature académique surabondante sur la gestion des arbres, que la plupart des exemples d'implémentation sont faits en C/C++ : pourquoi ? Tout simplement parce que, d'une part, à la différence du C#/.Net, le C/C++ supporte depuis son origine des variables et méthodes membres « statiques » au niveau de la méthode, alors que le C# ne les supporte qu'au niveau de la classe ; d'autre part, le C/C++ supporte des pointeurs génériques, et bien que le C# les supporte, il m'a semblé plus prudent de stocker le père d'un nœud non pas via un pointeur, mais dans une structure anonyme du type :
public struct TreeNode {
public int level;
public int rank;
public int owner_node;
public T theValue;
}En quoi ceci est-il si important ? Parce que pour résoudre le problème technique central de l'arbre (nous ne connaissons ni sa « profondeur », ni le nombre de ses nœuds, tous les deux étant dynamiques et en principe non bornés) il faut une « ruse » pour gérer cela, et cette ruse est en réalité assez simple : utiliser des méthodes récursives qui manipulent des structures statiques, et des variables d'état statiques, afin d'empiler « à l'infini » des nœuds intermédiaires lors de notre parcours de l'arbre.
Si vous croyez donc que la récursivité est une chose peu utile dont n'y adhèrent que les universitaires, vous avez tort : tout algorithme qui doit « stocker » des informations qui seront traitées « à leur tour » et dans un ordre inconnu tire parti efficacement de la récursivité. Utiliser la récursivité pour calculer un factoriel ne m'a jamais enchanté (très « vieille école », je préfère le calcul itératif pour les tâches triviales, car propre et facilement lisible), mais pour les arbres, entre autres, elle est quasi indispensable.
L'enjeu principal de la récursivité ? Savoir quand il faut s'arrêter d'appeler la méthode récursive, pour que cela ne « cycle » pas, c'est-à-dire n'entre pas dans une boucle infinie si aucune solution n'est trouvée ; j'ai tenté de mettre les garde-fous nécessaires dans mon code pour empêcher qu'une méthode « cycle ».
Il y a aussi la question des optimisations : certaines optimisations sont très simples ; soit un arbre d'un million de pièces, où on veut trouver les descendants de la pièce « XYZ » : la première chose à faire, avant même d'effectuer un parcours récursif, c'est de vérifier que la pièce existe, pour éviter un parcours inutile. Quand cela me semblait pertinent, j'ai rajouté ces tests qui optimisent le code.
Certains disent donc que le C/C++ est plus adapté à la gestion des arbres, car la gestion des structures statiques est mieux faite et plus souple, mais je ne suis pas de cet avis : vous verrez que dans notre implémentation vous ne déclarez ni ne manipulez des structures statiques dans le C# : cela est fait pour vous dans les constructeurs de la classe principale. Qui plus est, l'exceptionnelle richesse et rapidité des génériques modèles qui existent en natif dans le CLR compense largement cet inconvénient.
Vous remarquerez que j'ai fait le choix d'encapsuler toutes les structures et variables statiques, au prix d'un appel obligatoire à ma méthode void reinitializeTrees(); l'alternative m'aurait contraint de rajouter des structures statiques dans la signature de mes principales méthodes, mais cette option me paraissait inélégante et contraire aux principes de l'encapsulation.
Bien évidemment, toute cette complexité est cachée : le développeur se contentera d'utiliser les membres définis dans l'interface.
Mais il y a un effet négatif qui est une conséquence du caractère statique de la gestion via des « statiques » : il faut impérativement « nettoyer » les structures statiques (ou bien les réallouer à une nouvelle instance) entre chaque « parcours » de l'arbre, et cela est illustré dans les exemples d'appel fournis dans le driver.
Il y a des alternatives à la solution que je vous propose, et notamment le stockage des nœuds dans un document XML, avec des accesseurs en XSLT et des contrôles en XSD, mais à mon avis, la solution que je vous propose est plus efficace (par plusieurs ordres de grandeur !) et est sensiblement plus souple. L'approche XML pour moi vient, en fait, « en aval » de notre solution, car il est assez facile de mettre au format XML ou HTML le résultat d'un query du type :
List<Tree<T>.TreeNode> traverseByAddressFull()On peut ainsi l'intégrer sans complication dans une page web ou un Web Service.
III. Description de l'Implémentation▲
L'objectif de mon implémentation, c'est de produire une bibliothèque du style .dll ou .lib (si vous utilisez occasionnellement, comme moi, les frameworks Mono sous Unix). On peut utiliser n'importe quelle version de Visual Studio : voir l'en-tête des sources pour une description des prérequis.
La solution que nous avons fournie se décompose en cinq fichiers source : un qui décrit les interfaces formelles, et un qui implémente les interfaces. Deux fichiers décrivent, l'un l'interface des méthodes de tri paramétrable, l'autre l'implémentation des routines de tri. Ce sont ces quatre fichiers qui doivent produire le « Trees.ddl » que vous inclurez et référencerez dans votre projet « Visual Studio ».
Le fichier TestTreeDriver.cs est hyper utile, mais il n'est pas nécessaire pour générer un DLL sous Windows ou avec Mono : il s'agit d'un « driver », avec une méthode Main(), qui permet de démontrer simplement -- ou plutôt tester -- toutes les fonctionnalités de l'interface, à travers des exemples pédagogiques.
Ainsi, dans la solution (.sln) actuelle que vous pouvez facilement télécharger à l'adresse suivante : https://dotnet.developpez.com/telecharger/detail/id/4324/Gestion-des-Arbres-en-C-Net il s'agit d'un projet du type « console exécutable », ne faisant pas appel à l'indispensable framework de tests dont on a besoin dans le monde réel : la solution actuelle peut être transformée en simple « bibliothèque DLL » en moins d'une minute. En quelques clics, il suffit de télécharger la solution, cliquer le fichier de solution « Trees.sln », puis builder, afin de déboguer et tester le driver.
Il vous restera ensuite à mettre tous mes tests du driver actuel dans un framework de tests du type N-Unit.
Il est possible que vous ayez besoin de modifier le code, afin de modifier le comportement de la bibliothèque : à titre d'exemple, j'ai expliqué au début de cet article que chaque nœud de mon arbre stocke une clef non unique, mais il est possible que votre arbre n'autorise que des clefs uniques, et cela nécessitera des modifications dans mes méthodes de validation, mais si mon travail est bien fait, il n'y aura pas de modifications à effectuer dans les structures que je manipule.
Comme il se doit, tout est dit dans l'interface, dont la description suit. Si on comprend bien l'interface, on sera à même de l'étendre en cas de besoin, soit :
// Implementation File : TreeImplementation.cs
// -------------------------------------------
using System;
using System.Collections.Generic;
using System.Linq;
namespace your_inverted_domain.utilities.trees
{
// All Interface Members:
public interface ITree<T>
{
int countElementsInTree();
int count { get; set; }
Tree<T>.TreeNode originValue { get; set; }
T[] getValues();
List<T> getValuesList();
int addNodeToTree(int level, int rank, int owner_node, T newElement);
int updateNodeInTree(int level, int rank, int owner_node, T modifiedElement);
bool getIsUniqueValue(T inputValue);
Tree<T>.TreeNode getNodeFromUniqueValue(T inputValue);
T getNodeValueByAddress(int level, int rank, int owner_node);
int[] getNodeAddressFromUniqueValue(T inputValue);
bool deleteLeafNodeByAddress(int level, int rank, int owner_node);
bool deleteLeafNodeByUniqueValue(T value);
List<Tree<T>.TreeNode> getAllNodes();
int getMaxDepth();
int getMaxWidthAtLevel(int level);
List<Tree<T>.TreeNode> traverseByAddressFull(int? level, int? rank, int? owner_node, T theValue);
List<Tree<T>.TreeNode> traverseByUniqueFull(T theValue);
List<Tree<T>.TreeNode> traverseByAddressOneLevel(int? level, int? rank, int? owner_node, T theValue);
List<Tree<T>.TreeNode> traverseByUniqueOneLevel(T theValue);
List<Tree<T>.TreeNode> ascendByAddress(int? level, int? rank, int? owner_node, T theValue);
List<Tree<T>.TreeNode> ascenByUnique(T theValue);
bool deleteBranchInTreeByNode(Tree<T>.TreeNode value, Tree<T> myTree);
void reinitializeTrees();
}
}Quant à l'interface pour les tris, c'est simple, avec quatre variantes de la méthode Compare() :
using System;
using System.Collections.Generic;
using System.Linq;
namespace your_inverted_domain.utilities.trees
{
public interface IComparer<T>
{
int Compare(Tree<T>.TreeNode x, Tree<T>.TreeNode y);
}
}Si vous déboguez le code, vous constaterez que les méthodes récursives ne sont pas « Tail Recursion », c'est-à-dire qu'il y a un empilement des appels de fonction, avec pour résultat, à première vue assez bizarre, que le statement « return » ne renvoie pas le résultat et ne « sort pas », et c'est un peu déroutant au début, même si le résultat final est correct.
Il y a une solution qui s'articule autour du «trampolining» pour faire (une simulation) de la « Tail Recursion » en C#, mais qui n'est pas nécessaire dans le cas de notre implémentation. On peut espérer qu'une future CLR.Net comprendra une annotation C# du type :
[TailRecursion]Après avoir testé mon implémentation des arbres, je me suis rendu compte que, pour de très grands arbres, il aurait été intéressant de faire persister sur disque l'image d'un arbre, afin de ne pas avoir à le recréer de toutes pièces au démarrage d'une application : cela plairait, par exemple, aux gestionnaires de portefeuilles qui gèrent des « métaportefeuilles » (un portefeuille contenant d'autres sous-portefeuilles, chacun avec des milliers de titres), car cela permet de faire des simulations d'impact très rapides, sans avoir à recréer l'arbre de toutes pièces.
C'est la Sérialisation.Net qui est parfaitement adaptée à cette tâche.
Quand cela m'a semblé utile -- et notamment pour les algorithmes un peu complexes -- j'ai commenté le code pour que le lecteur l'appréhende mieux.
IV. Remerciements▲
Merci à Steve Begelman pour la rédaction de ce tutoriel et à FRANOUCH pour sa relecture orthographique. Nous remercions également les membres de la Rédaction de Developpez pour le travail de gabarisation et de relecture qu'ils ont effectué, en particulier :